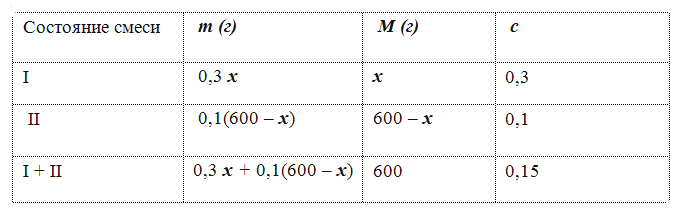Алгебраический метод решения задач или задачи, которые решаются с помощью уравнения.
Основные этапы решения задач
1. Выбор неизвестной (или неизвестных).
2. Выбор чистого вещества.
3. Переход к долям.
4. Отслеживание состояния смеси.
5. Составление уравнения.
6. Решение уравнения (или их системы).
7. Формирование ответа.
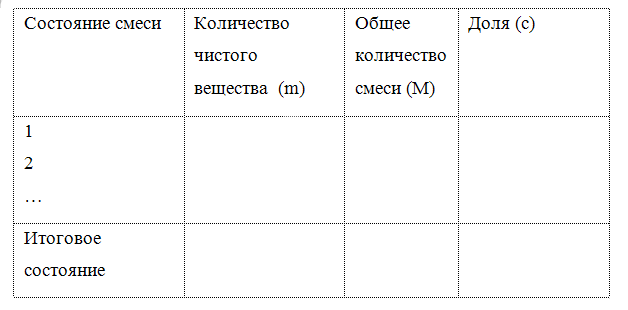
В ходе осуществления этих этапов рекомендуется ввести следующую таблицу:
Задача. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация составляла 1,5%?
Решение.
1. Пусть требуется добавить x кг пресной воды.
2. За чистое вещество примем соль. Тогда морская вода - это смесь с 5%-ным содержанием чистого вещества, пресная вода - с 0%-ным содержанием чистого вещества.
3. Переходя долям, получаем, что доля соли в морской воде составляет 0,05, доля соли в пресной воде равна 0, доля в смеси, которую нужно получить, - 0,015.
4.Происходит соединение смесей
5. Исходя из третьей строки таблицы, составим уравнение
m = с M :
0,05 · 30 = 0,015(30 + x).
6. Решим полученное уравнение и находим x = 70.
7. В данной задаче не содержалось требования найти процентное содержание какого-либо вещества, поэтому нет необходимости переводить доли в процентные содержания.
Ответ: 70 кг.
Задача. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 600 г 15%-ного раствора. Сколько граммов каждого вещества было взято?
Решение: Пусть взяли x г первого раствора, тогда второго раствора (600 - x) г.
Тогда 0,3 x + 0,1(600 - x) = 0,15 · 600, откуда x = 150, 600 - x = 450.
Ответ: 150 г 30%-ного раствора,
450 г 10%-ного раствора.
Задача. Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 25% цинка, а второй - 50% меди. Процентное содержание олова в первом сплаве в 2 раза выше, чем во втором. Сплавив 200 кг первого и 300 кг второго, получили новый сплав, в котором оказалось 28% олова. Определить, сколько килограммов меди содержится в получившемся новом сплаве.
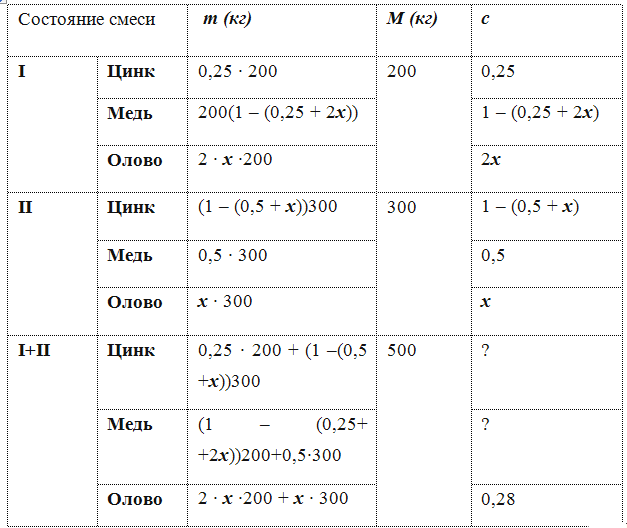
Решение. Пусть x - доля олова во II сплаве, тогда 2x - доля олова в I сплаве. Сначала определим долю олова в данных сплавах. Для этого заполним таблицу, выполнив переход от процентных содержаний к долям.
Становится очевидным, что уравнение можно составить по последней строке таблицы, используя зависимость m = с M :
2 · x · 200 + x · 300 = 0,28 · 500, откуда x = 0,2.
Таким образом, доля олова в первом сплаве будет 0,4, а во втором - 0,2.
Теперь выберем в качестве чистого вещества медь, и пусть y - доля меди в получившемся сплаве.
Сосчитаем по таблице долю меди в первом сплаве
1 - (0,25 + 0,4) = 0,35.
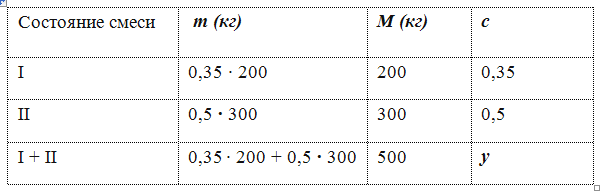
Составим таблицу (относительно меди).
Составим уравнение по последней строке таблицы, используя зависимость
m = с M :
0,35 · 200 + 0,5 · 300 = 500y. Находим y = 0,44.
Доля меди в получившемся сплаве - 0,44. Выполним требование задачи и найдем количество меди: m = 500 · 0,44 = 220.
Ответ: 220 кг.
Данный метод является универсальным и с помощью него решается любая задача по данной теме.